OPERACIONES CON NUMEROS ENTEROS
OPERACIONES CON NUMEROS ENTEROS
¿Qué es un número entero?
Recordemos que los números naturales, , son los números que usamos para contar (sin decimales):
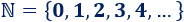
Los números enteros, , son los números naturales con signo (positivo y negativo), excepto el número , que no tiene signo:
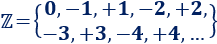
Es habitual escribir los enteros positivos sin signo, a no ser que sea necesario.
Observa que el conjunto de los números naturales está contenido en el conjunto de los números enteros:
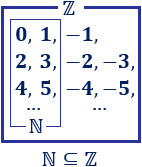
Suma de números enteros
Si los dos enteros a sumar tienen el mismo signo, se suman los números (sin signo) y se conserva el signo.
Ejemplo
Sumamos los enteros y :
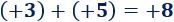
Sumamos los enteros y :
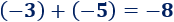
Si los dos enteros tienen signos distintos, se restan los números (sin signo) y se conserva el signo del número que sea mayor (sin signo).
Ejemplo
Sumamos los enteros y :
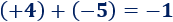
Sumamos los enteros y :
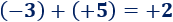
Resta de números enteros
Cuando tenemos una resta de enteros, podemos transformarla en una suma cambiando el signo del segundo sumando.
Ejemplo
Restamos los enteros y :
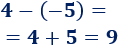
Restamos los enteros y :
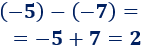
Restamos los enteros y :
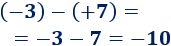
Regla de los signos
La regla de los signos proporciona el signo del resultado de la multiplicación/división de dos enteros:
- El resultado es positivo si los dos factores tienen el mismo signo.
- El resultado es negativo si los dos factores tienen signo distinto.
- El resultado es neutro si alguno de los factores es .
Podemos resumir la regla como sigue:
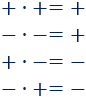
Multiplicación/división de enteros
La multiplicación de dos enteros se calcula multiplicando los números (sin signo) y aplicando la regla de los signos.
Ejemplo
Multiplicamos los enteros y :
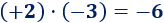
Multiplicamos los enteros y :
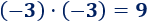
Multiplicamos los enteros y :
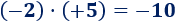
Multiplicamos los enteros y :
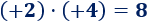
La división de enteros se calcula dividiendo los números (sin signo) y aplicando la regla de los signos.
Ejemplo
Dividimos los enteros y :
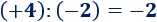
Dividimos los enteros y :
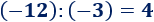
Operaciones combinadas con números enteros
Las operaciones combinadas o mixtas son operaciones compuestas por varias operaciones (sumas, restas, multiplicaciones y/o divisiones).
En estas operaciones, la multiplicación y la división tienen prioridad sobre la suma y la resta. Los paréntesis pueden utilizarse para cambiar este orden.
Ejemplo
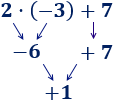
Hemos calculado la multiplicación y, después, la suma.
Ejemplo
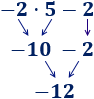
Hemos calculado la multiplicación y, después, la suma.
Ejemplo
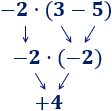
En esta operación, hemos calculado primero la resta porque había un paréntesis: el multiplica al resultado de la resta del paréntesis.
Ejemplo
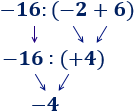
En esta operación, hemos calculado primero la suma porque había un paréntesis: el tiene que dividirse entre el resultado de la suma del paréntesis.







0 comentarios: